Methods to Calculate Cosine Similarity in Python?

Introduction

This text will focus on cosine similarity, a device for evaluating two non-zero vectors. Its effectiveness at figuring out the orientation of vectors, no matter their dimension, results in its in depth use in domains equivalent to textual content evaluation, knowledge mining, and info retrieval. This text explores the arithmetic of cosine similarity and exhibits the right way to use it in Python.

Overview: 

• Find out how cosine similarity measures the angle between two vectors to check their orientation successfully.
• Uncover the functions of cosine similarity in textual content evaluation, knowledge mining, and suggestion programs.
• Perceive the mathematical basis of cosine similarity and its sensible implementation utilizing Python.
• Acquire insights into implementing cosine similarity with NumPy and scikit-learn libraries in Python.
• Discover how cosine similarity is utilized in real-world eventualities, together with doc comparability and suggestion programs.

What’s Cosine Similarity?

Cosine similarity measures the cosine of the angle between two vectors in a multi-dimensional house. The cosine of two non-zero vectors may be derived through the use of the Euclidean dot product formulation:

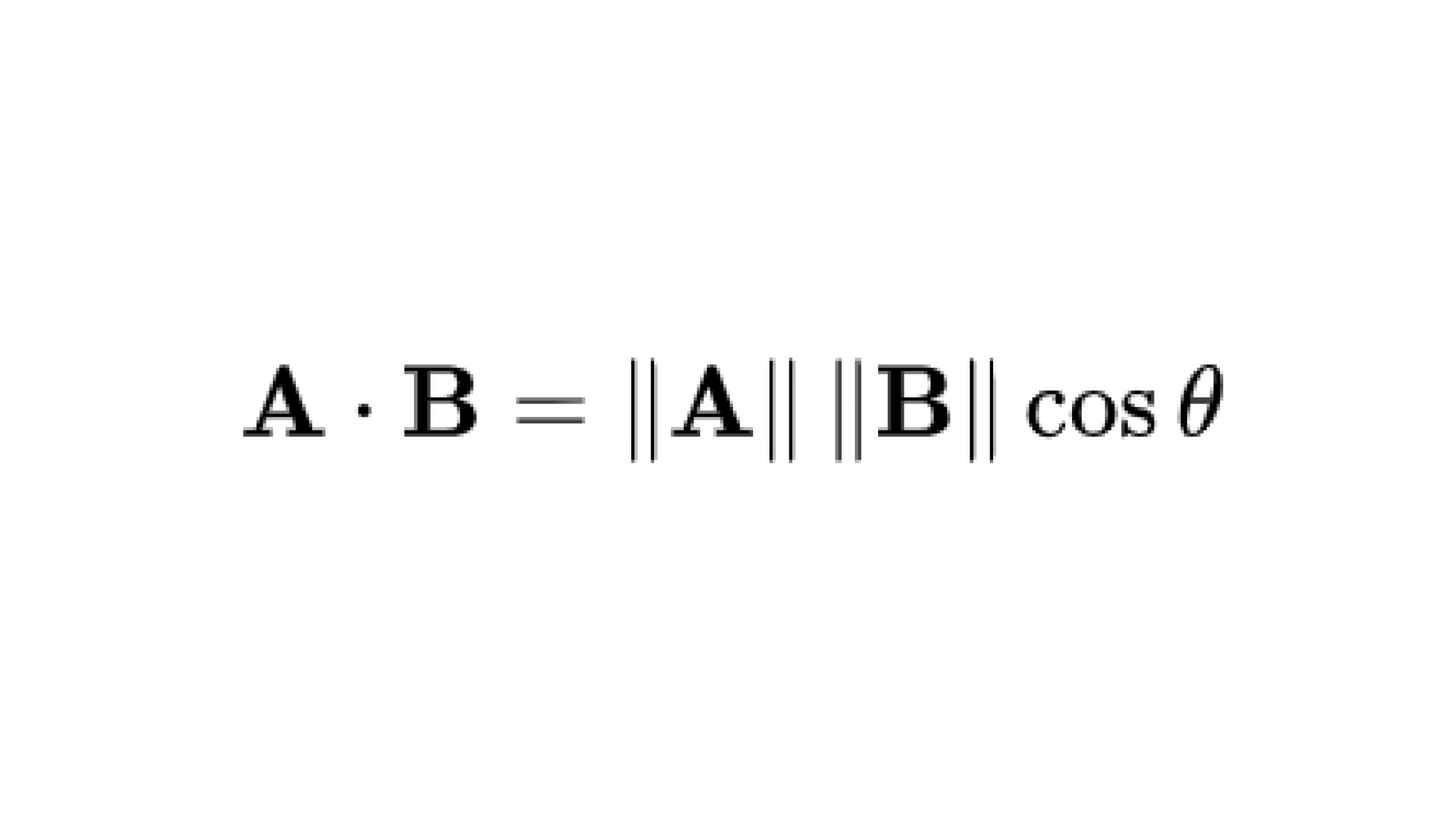
Given two n-dimensional vectors of attributes, A and B, the cosine similarity, cos(θ), is represented utilizing a dot product and magnitude as

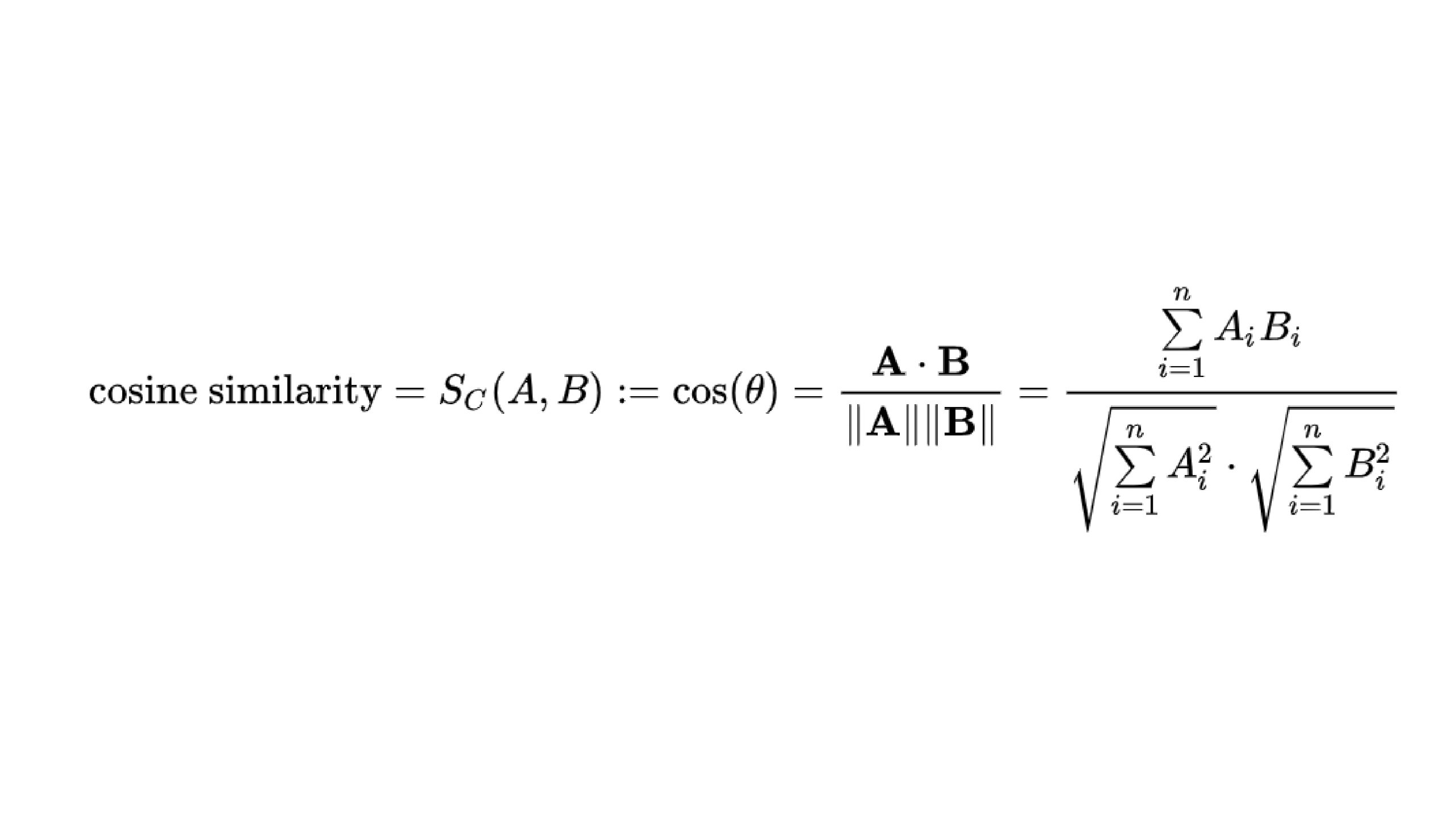
The cosine similarity ranges from -1 to 1, the place:

• 1 signifies that the vectors are similar,
• 0 signifies that the vectors are orthogonal (no similarity),
• -1 signifies that the vectors are diametrically opposed.

Purposes in Information Science

• Textual content similarity: In NLP, we use cosine similarity to grasp doc similarities. We rework texts in these paperwork into TF-IDF vectors after which use cosine similarity to seek out their similarities.
• Advice Methods: Let’s say we have now a music suggestion system. Right here, we calculate the similarity between customers, and primarily based on the rating, we propose songs or music to different customers. Typically, suggestion programs use cosine similarity in collaborative filtering or different filtering methods to recommend gadgets for our customers.

Implementation of Cosine Similarity

Allow us to now learn to implement cosine similarity utilizing totally different libraries:

Implementation Utilizing Numpy Library

# Utilizing numpy
import numpy as np

# Outline two vectors
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])

# Compute cosine similarity
cos_sim = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
print("Cosine Similarity (NumPy):", cos_sim)

Right here, we’re creating two arrays, A and B, which is able to act because the vectors we have to examine. We use the cosine similarity formulation, i.e., the dot product of A and B upon mod of A X mod B.

Implementation Utilizing Scikit-learn Library

from sklearn.metrics.pairwise import cosine_similarity

# Outline two vectors
A = [[1, 2, 3]]
B = [[4, 5, 6]]

# Compute cosine similarity
cos_sim = cosine_similarity(A, B)
print("Cosine Similarity (scikit-learn):", cos_sim[0][0])

Right here, we are able to see that the inbuilt operate within the sklearn library does our job of discovering the cosine similarity.

Step-By-Step Arithmetic Behind the Numpy Code

Conclusion

Cosine similarity is a robust device for locating the similarity between vectors, significantly helpful in high-dimensional and sparse datasets. On this article, we have now additionally seen the implementation of cosine similarity utilizing Python, which may be very simple. We have now used Python’s NumPy and scikit-learn libraries to implement cosine similarity. Cosine similarity is necessary in NLP, textual content evaluation, and suggestion programs as a result of it’s unbiased of the magnitude of the vector.

Ceaselessly Requested Questions