[ad_1]
Introduction
Assume you might be engaged in a difficult undertaking, like simulating real-world phenomena or creating a complicated neural community to forecast climate patterns. Tensors are advanced mathematical entities that function behind the scenes and energy these refined computations. Tensors effectively deal with multi-dimensional information, making such revolutionary initiatives doable. This text goals to offer readers with a complete understanding of tensors, their properties, and purposes. As a researcher, skilled, or scholar, having a strong understanding of tensors will aid you take care of advanced information and superior pc fashions.
Overview
- Outline what a tensor is and perceive its numerous varieties and dimensions.
- Acknowledge the properties and operations related to tensors.
- Apply tensor ideas in numerous fields resembling physics and machine studying.
- Carry out fundamental tensor operations and transformations utilizing Python.
- Perceive the sensible purposes of tensors in neural networks.
What’s Tensor?
Mathematically, tensors are objects that stretch matrices, vectors, and scalars to greater dimensions. The domains of pc science, engineering, and physics are all closely depending on tensors, particularly in relation to deep studying and machine studying.
A tensor is, to place it merely, an array of numbers with doable dimensions. The rank of the tensor is the variety of dimensions. That is a proof:
- Scalar: A single quantity (rank 0 tensor).
- Vector: A one-dimensional array of numbers (rank 1 tensor).
- Matrix: A two-dimensional array of numbers (rank 2 tensor).
- Larger-rank tensors: Arrays with three or extra dimensions (rank 3 or greater).
Mathematically, a tensor could be represented as follows:
- A scalar ( s ) could be denoted as ( s ).
- A vector ( v ) could be denoted as ( v_i ) the place ( i ) is an index.
- A matrix ( M ) could be denoted as ( M_{ij} ) the place ( i ) and ( j ) are indices.
- A better-rank tensor ( T ) could be denoted as ( T_{ijk…} ) the place ( i, j, okay, ) and many others., are indices.
Properties of Tensors
Tensors have a number of properties that make them versatile and highly effective instruments in numerous fields:
- Dimension: The variety of indices required to explain the tensor.
- Rank (Order): The variety of dimensions a tensor has.
- Form: The scale of every dimension. For instance, a tensor with form (3, 4, 5) has dimensions of three, 4, and 5.
- Sort: Tensors can maintain several types of information, resembling integers, floating-point numbers, and many others.
Tensors in Arithmetic
In arithmetic, tensors generalize ideas like scalars, vectors, and matrices to extra advanced constructions. They’re important in numerous fields, from linear algebra to differential geometry.
Instance of Scalars and Vectors
- Scalar: A single quantity. For instance, the temperature at some extent in area could be represented as a scalar worth, resembling ( s = 37 ) levels Celsius.
- Vector: A numerical array with magnitude and path in a single dimension. For instance, a vector (v = [3, 4, 5]) can be utilized to explain the rate of a shifting object, the place every ingredient represents the rate element in a selected path.
Instance of Tensors in Linear Algebra
Take into account a matrix ( M ), which is a two-dimensional tensor:

Multi-dimensional information, resembling a picture with three coloration channels, could be represented by advanced tensors like rank-3 tensors, whereas the matrix is used for transformations like rotation or scaling vectors in a aircraft. Dimensions are associated to depth of coloration, width, and peak.
Tensor Contraction Instance
Tensor contraction is a generalization of matrix multiplication. For instance, if we’ve two matrices ( A ) and ( B ):
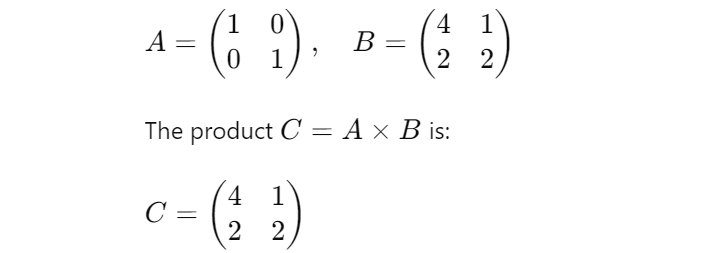
Right here, the indices of ( A ) and ( B ) are summed over to supply the weather of ( C ). This idea extends to higher-rank tensors, enabling advanced transformations and operations in multi-dimensional areas.
Tensors in Laptop Science and Machine Studying
Tensors are essential for organizing and analyzing multi-dimensional information in pc science and machine studying, particularly in deep studying frameworks like PyTorch and TensorFlow.
Information Illustration
Tensors are used to signify numerous types of information:
- Scalars: Represented as rank-0 tensors. As an example, a single numerical worth, resembling a studying charge in a machine studying algorithm.
- Vectors: Represented as rank-1 tensors. For instance, an inventory of options for an information level, resembling pixel intensities in a grayscale picture.
- Matrices: As rank-2 tensor representations. incessantly used to carry datasets by which a characteristic is represented by a column and an information pattern by a row.
- Larger-Rank Tensors: Utilized with extra intricate information codecs. As an example, a rank-3 tensor with dimensions (peak, width, channels) can be utilized to signify a coloration picture.
Tensors in Deep Studying
In deep studying, tensors are used to signify:
- Enter Information: Uncooked information fed into the neural community. As an example, a batch of photographs could be represented as a four-dimensional tensor with form (batch measurement, peak, width, channels).
- Weights and Biases: Parameters of the neural community which are discovered throughout coaching. These are additionally represented as tensors of applicable shapes.
- Intermediate Activations: Outputs of every layer within the neural community, that are additionally tensors.
Instance
Take into account a easy neural community with an enter layer, one hidden layer, and an output layer. The information and parameters at every layer are represented as tensors:
import torch
# Enter information: batch of two photographs, every 3x3 pixels with 3 coloration channels (RGB)
input_data = torch.tensor([[[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[9, 8, 7], [6, 5, 4], [3, 2, 1]],
[[0, 0, 0], [1, 1, 1], [2, 2, 2]]],
[[[2, 3, 4], [5, 6, 7], [8, 9, 0]],
[[0, 9, 8], [7, 6, 5], [4, 3, 2]],
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]]])
# Weights for a layer: assuming a easy totally related layer
weights = torch.rand((3, 3, 3, 3)) # Random weights for demonstration
# Output after making use of weights (simplified)
output_data = torch.matmul(input_data, weights)
print(output_data.form)
# Output: torch.Dimension([2, 3, 3, 3])Right here, input_data is a rank-4 tensor representing a batch of two 3×3 RGB photographs. The weights are additionally represented as a tensor, and the output information after making use of the weights is one other tensor.
Tensor Operations
Widespread operations on tensors embrace:
- Component-wise operations: Operations utilized independently to every ingredient, resembling addition and multiplication.
- Matrix multiplication: A particular case of tensor contraction the place two matrices are multiplied to supply a 3rd matrix.
- Reshaping: Altering the form of a tensor with out altering its information.
- Transposition: Swapping the size of a tensor.
Representing a 3×3 RGB Picture as a Tensor
Let’s contemplate a sensible instance in machine studying. Suppose we’ve a picture represented as a three-dimensional tensor with form (peak, width, channels). For a coloration picture, the channels are normally Pink, Inexperienced, and Blue (RGB).
# Create a 3x3 RGB picture tensor
picture = np.array([[[255, 0, 0], [0, 255, 0], [0, 0, 255]],
[[255, 255, 0], [0, 255, 255], [255, 0, 255]],
[[128, 128, 128], [64, 64, 64], [32, 32, 32]]])
print(picture.form)
Right here, picture is a tensor with form (3, 3, 3) representing a 3×3 picture with 3 coloration channels.
Implementing a Primary CNN for Picture Classification
In a convolutional neural community (CNN) used for picture classification, an enter picture is represented as a tensor and handed by means of a number of layers, every reworking the tensor utilizing operations like convolution and pooling. The ultimate output tensor represents the chances of various courses.
import torch
import torch.nn as nn
import torch.nn.purposeful as F # Importing the purposeful module
# Outline a easy convolutional neural community
class SimpleCNN(nn.Module):
def __init__(self):
tremendous(SimpleCNN, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.fc1 = nn.Linear(16 * 3 * 3, 10)
def ahead(self, x):
x = self.pool(F.relu(self.conv1(x))) # Utilizing F.relu from the purposeful module
x = x.view(-1, 16 * 3 * 3)
x = self.fc1(x)
return x
# Create an occasion of the community
mannequin = SimpleCNN()
# Dummy enter information (e.g., a batch of 1 grayscale picture of measurement 8x8)
input_data = torch.randn(1, 1, 8, 8)
# Ahead cross
output = mannequin(input_data)
print(output.form)
A batch of pictures is represented by the rank-4 tensor input_data on this instance. These tensors are processed by the convolutional and totally related layers, which apply completely different operations to them with the intention to generate the specified outcome.
Conclusion
Tensors are mathematical constructions that carry matrices, vectors, and scalars into greater dimensions. They’re important to theoretical physics and machine studying, amongst different domains. Professionals working in deep studying and synthetic intelligence want to know tensors with the intention to use up to date computational frameworks to progress analysis, engineering, and know-how.
Steadily Requested Questions
A. A tensor is a mathematical object that generalizes scalars, vectors, and matrices to greater dimensions.
A. The rank (or order) of a tensor is the variety of dimensions it has.
A. Tensors are used to signify information and parameters in neural networks, facilitating advanced computations.
A. One widespread tensor operation is matrix multiplication, the place two matrices are multiplied to supply a 3rd matrix.
[ad_2]