Introduction to Log-normal Distribution

Introduction

The log-normal distribution is an interesting statistical idea generally used to mannequin information that exhibit right-skewed habits. This distribution has wide-ranging functions in varied fields, equivalent to biology, finance, and engineering. On this article, we’ll delve into the log-normal distribution, its key parameters, and how you can interpret them, in addition to discover some sensible examples to boost understanding.

Overview

• A log-normal distribution fashions information the place the pure logarithm of a variable follows a standard distribution, exhibiting optimistic skewness.
• Perceive the form (σ), scale (m or eμ), and site (μ) parameters to interpret and apply the log-normal distribution.
• The log-normal distribution is linked to the conventional distribution; if X is log-normal, ln(X) is often distributed, and vice versa.
• Estimate parameters μ σ from information utilizing strategies like Most Chance Estimation, which includes log transformation and calculating the imply and customary deviation.
• The log-normal distribution is broadly utilized in biology, finance, reliability engineering, and environmental science to mannequin right-skewed information equivalent to progress charges, inventory costs, and time to failure.

What’s a Log-normal Distribution?

A log-normal distribution describes the chance distribution of a random variable when its logarithm follows a standard distribution. In easier phrases, if the pure logarithm of a variable X follows a standard distribution, then X follows a log-normal distribution. This distribution stays steady and options optimistic skewness, that means it has an extended proper tail.

Key Parameters

There are primarily three parameters as follows:

1. Form Parameter (σ): This parameter impacts the overall form of the distribution. It is usually the usual deviation of the log-transformed variable.
2. Scale Parameter (m or eμ): This parameter stretches or shrinks the distribution’s graph. On this distribution, the size parameter is commonly known as the median.
3. Location Parameter (μ): This parameter determines the place on the x-axis the graph is situated. It’s the imply of the log-transformed variable.

These parameters are important in understanding how this distribution behaves and the way it may be utilized to real-world information.

Additionally Learn: What’s Regular Distribution : An Final Information

Chance Density Perform

The chance density operate (PDF) of a log-normal distribution is given by:

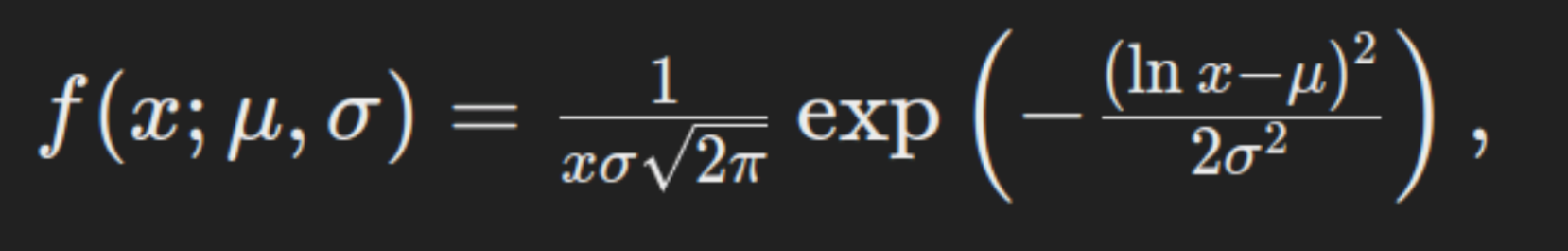
the place x>0, μ is the imply of the variable’s logarithm, and σ is the usual deviation of the variable’s logarithm. This method exhibits that the log-normal distribution is outlined for optimistic values solely, because the logarithm will not be outlined for non-positive values.

Relationship with the Regular Distribution

One of the vital attention-grabbing facets of its relationship with the conventional distribution. If X follows a log-normal distribution, Y = ln(X) follows a standard distribution. Conversely, if Y follows a standard distribution, X = eY follows a log-normal distribution. This relationship permits us to make use of well-established strategies for regular distributions to research log-normal information by reworking the information utilizing logarithms.

Calculating Parameters from Knowledge

We frequently use strategies equivalent to Most Chance Estimation (MLE) to estimate the parameters of this type of distribution from information. Right here’s a simplified strategy to estimate μ and σ:

1. Log-transform the information: Take the pure logarithm of all information factors.
2. Calculate the log-transformed information’s pattern imply and customary deviation: These statistics would be the estimates for μ and σ.

For instance, take into account a dataset of log-normally distributed incomes. By taking the pure logarithm of every earnings, we are able to compute the imply and customary deviation of those log-transformed values to estimate μ and σ.

Sensible Functions

This distribution is broadly utilized in varied fields attributable to its means to mannequin skewed information. Listed below are some examples:

1. Biology: In organic research, organisms’ progress charges typically comply with a log-normal distribution as a result of progress charges are multiplicative slightly than additive.
2. Finance: Inventory costs are generally modeled utilizing log-normal distributions as a result of the proportion change in costs is often distributed.
3. Reliability Engineering: The time to failure of sure merchandise will be modeled utilizing a log-normal distribution, particularly when the failure course of is multiplicative.
4. Environmental Science: The distribution of particle sizes in aerosols or the quantity of rainfall in a given interval.

Instance Calculation

Let’s take into account a sensible instance to calculate the parameters of a log-normal distribution. Assume now we have the next earnings information (in 1000’s): 20, 22, 25, 27, 30.

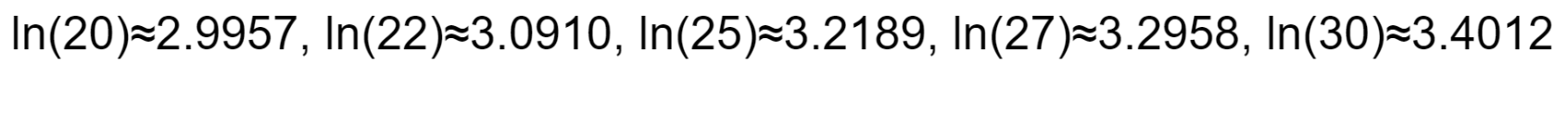
• Calculate the pattern imply μ:

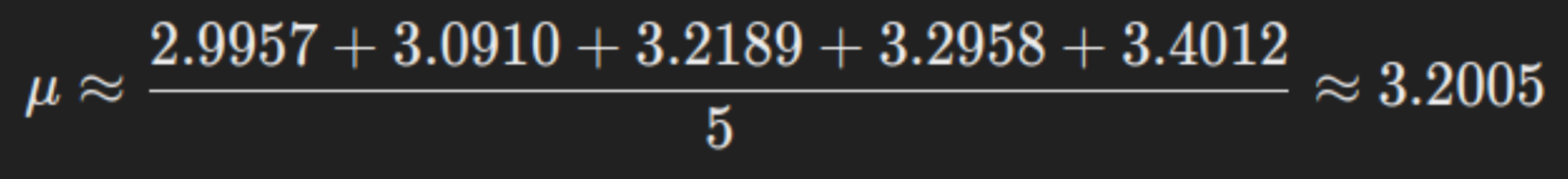
• Calculate the pattern customary deviation (σ):

Thus, the estimated parameters for the log-normal distribution are μ approx 3.2005 and σ approx 0.1504.

Deciphering the Parameters

• μ: That is the imply of the log-transformed information. In our instance, a μ of three.2005 signifies that the common of the pure logarithms of the incomes is round this worth.
• σ: That is the usual deviation of the log-transformed information. A σ of 0.1504 means that the log-transformed incomes are comparatively near the imply on a logarithmic scale.

Conclusion

The log-normal distribution is a strong instrument for modeling right-skewed information. We are able to successfully analyze and interpret information in varied fields by understanding its key parameters and their relationship with the conventional distribution. Whether or not coping with monetary information, organic progress charges, or reliability metrics, it gives a strong framework for understanding and predicting habits.

Often Requested Questions